Teoria dos Jogos: Uma Abordagem Acadêmica para os Desafios do Desenvolvimento na Amazônia
Por Estevão Monteiro de Paula
______________________________
Introdução
A Teoria dos Jogos é uma ferramenta poderosa que pode ser aplicada em diversos contextos para entender e resolver problemas complexos. Este artigo explora a aplicação da Teoria dos Jogos sobre a Amazônia, abrangendo tanto as situações práticas dentro da região quanto o desenvolvimento de estratégias e políticas para o benefício sustentável da Amazônia.
Por um lado, a Teoria dos Jogos na Amazônia nos permite analisar as interações entre diferentes atores, como comunidades indígenas, empresas e governos, ajudando a prever comportamentos e resultados em cenários específicos. Por outro lado, a Teoria dos Jogos para a Amazônia envolve a criação de políticas públicas e estratégias que incentivem a cooperação e a sustentabilidade, visando a preservação ambiental e o desenvolvimento econômico da região.
Ao combinar essas duas abordagens, este artigo busca fornecer uma visão abrangente de como a Teoria dos Jogos pode contribuir para a conservação e o desenvolvimento sustentável da Amazônia, promovendo soluções que beneficiem todos os envolvidos.
O que é a teoria dos jogos
A Teoria dos Jogos é um ramo da matemática e da economia que estuda interações estratégicas entre indivíduos chamados de “jogadores”. Os participantes dos jogos (jogadores), que podem ser indivíduos, empresas e governos se interagem com objetivos de maximizar seus próprios ganhos, levando em consideração as possíveis decisões dos outros jogadores.
Esta teoria contribui com formulações de estratégia para situações hipotéticas entre os participantes do jogo; ou seja, pode sugerir as ações que cada jogador pode tomar para conquistar resultados positivos com base na estratégia escolhida.
Pode-se, de certa forma, atribuir que esta teoria surge quase que naturalmente em consequência do jogo ser uma atividade fundamental para a cultura humana (Huizinga, 1938)[1].

A teoria dos jogos começou a ser discutida no século XVIII, com uma das primeiras contribuições significativas feitas pelo matemático britânico James Waldegrave em 1713. Waldegrave apresentou uma solução para o jogo de cartas “Le Her”, que era popular na França naquela época. Sua solução envolvia uma estratégia mista, onde os jogadores escolhiam aleatoriamente entre diferentes estratégias disponíveis em proporções específicas. Embora o trabalho de Waldegrave fosse básico em comparação com a teoria dos jogos moderna, ele foi uma das primeiras tentativas de abordar matematicamente a tomada de decisão em situações competitivas e incertas. Mais de dois séculos depois, John von Neumann e Oskar Morgenstern expandiram essa ideia em seu trabalho fundamental “Theory of Games and Economic Behavior” (1944)[2], considerado o marco da teoria moderna dos jogos.
No entanto, John Von Neumann e John Nash são considerados são considerados os matemáticos pioneiros da teoria dos jogos chamada de Equilíbrio Nash[3] que descreve uma situação em que nenhum jogador pode melhorar sua posição alterando sua estratégia unilateralmente. imita
Como o Ecossistema imita o Jogo
No ecossistema, assim como em um jogo, cada jogador tem um papel específico e segue certas regras para alcançar seu objetivo. Da mesma forma, cada organismo desempenha um papel importante e segue “regras” naturais para manter o equilíbrio. Ao observarmos a vida como um jogo de interações ecológicas, podemos compreender melhor a importância da cooperação, da competição e da adaptação, pois esses elementos são essenciais para a sobrevivência e o equilíbrio dos ecossistemas.
Enquanto os organismos lutam por recursos e se ajustam às condições ambientais, eles enfrentam desafios que garantem seu desenvolvimento e sobrevivência, de forma semelhante à maneira como os seres humanos enfrentam obstáculos em busca de objetivos. Essa interação entre organismos e ambientes mostra que a adaptação e o crescimento são processos inevitáveis e constantes. Assim, tanto na natureza quanto na vida humana, a capacidade de se adaptar e evoluir é essencial para prosperar diante das adversidades.
Nos anos 1950, John Nash desenvolveu o conceito de equilíbrio de Nash, aplicável a jogos não cooperativos. Durante essa década, a teoria dos jogos expandiu-se com conceitos como jogos na forma extensiva, jogador fictício e jogos repetidos. Reinhard Selten introduziu o equilíbrio perfeito em sub-jogo em 1965, e John Harsanyi desenvolveu jogos Bayesianos em 1967. Ambos, junto com Nash, ganharam o Prêmio Nobel de Economia em 1994.

Jogos na forma extensiva:
Na teoria dos jogos, os jogos na forma extensiva são representações que mostram as interações entre os jogadores de maneira sequencial, ou seja, passo a passo. Nessa forma, cada jogador toma decisões em momentos diferentes, e o resultado depende das escolhas feitas por todos os jogadores ao longo do jogo.
Esses jogos geralmente são ilustrados por árvores de decisão, onde cada ramificação representa uma escolha possível. Isso permite visualizar estratégias, consequências e resultados em várias fases, facilitando a análise de como as decisões de um jogador afetam os outros. Por exemplo: Imagine uma cadeia alimentar onde uma águia decide se caça um macaco-prego ou uma preguiça. Se a águia escolhe caçar o macaco-prego, o macaco deve decidir se foge ou se esconde. A decisão do macaco-prego, por sua vez, afeta a decisão da águia em futuras caçadas.
Jogador fictício:
Jogos fictícios, ou jogos de ficção, referem-se a jogos que envolvem narrativas, cenários e personagens que não existem na realidade. Esses jogos podem incluir elementos de fantasia, ficção científica, ou qualquer universo criado pela imaginação dos desenvolvedores.
Os jogos fictícios são comuns em diversas mídias, como videogames, RPGs (Role-Playing Games), e jogos de tabuleiro. Por exemplo: Os jogadores assumem o papel de líderes de uma pequena comunidade que se encontrará enfrentando os desafios das mudanças climáticas. O jogo se passa em um futuro próximo, onde as emissões de carbono, desastres naturais e a degradação ambiental ameaçam a sobrevivência da cidade.
Jogos repetidos:
Na teoria dos jogos, um jogo repetido é uma estrutura em que o mesmo jogo é jogado várias vezes, permitindo que os jogadores aprendam e ajustem suas estratégias com base nas experiências passadas. Isso contrasta com jogos de uma só rodada, onde as decisões são tomadas de forma isolada, sem a possibilidade de considerar jogadas anteriores. Por exemplo: Considere a relação entre flores e abelhas. As flores fornecem néctar e as abelhas polinizam as flores. Esse é um jogo repetido, onde a interação ocorre várias vezes ao longo do tempo.
Equilíbrio perfeito em sub-jogo (Reinhard Selten):
O Equilíbrio Perfeito em Sub-Jogos (EPSJ) é um conceito na teoria dos jogos que se aplica a jogos que podem ser representados por árvores de decisão. Esse conceito é uma extensão do Equilíbrio de Nash e é particularmente útil para analisar jogos dinâmicos e sequenciais, onde as escolhas de um jogador afetam as decisões e pagamentos futuros. Por exemplo: No ecossistema amazônico, duas espécies de árvores competem por recursos: a Espécie A, que cresce rapidamente, e a Espécie B, que possui um sistema radicular profundo.
Se ambas optam pelo crescimento rápido, competem intensamente por luz e acabam se estagnando. Porém, se uma escolhe crescer rapidamente enquanto a outra investe em raízes profundas, A captura a luz do sol enquanto B acessa a água e nutrientes no solo, permitindo que ambas coexistam de maneira equilibrada.
Esse cenário ilustra o conceito de Equilíbrio Perfeito em Sub-Jogos (EPSJ), onde as decisões de cada espécie impactam diretamente o sucesso da outra. Ao se adaptarem às escolhas do concorrente, as árvores encontram uma estratégia vantajosa que favorece a diversidade e a sustentabilidade do ecossistema.1.
Jogos Bayesianos (John Harsanyi):
Os Jogos bayesianos são um tipo de jogo em teoria dos jogos onde os jogadores têm informações incompletas sobre as características dos outros jogadores, como suas preferências, tipos ou estratégias. Nesses jogos, cada jogador possui crenças sobre as informações desconhecidas dos outros, e essas crenças são representadas por distribuições de probabilidade.
O ecossistema amazônico pode ser modelado como um jogo bayesiano envolvendo três grupos principais: madeireiros, conservacionistas e comunidades locais. Cada grupo possui interesses distintos e informações diferentes sobre os outros. Os madeireiros, por exemplo, podem ser divididos em dois tipos: os rigorosos, que seguem práticas sustentáveis, e os irresponsáveis, que buscam lucro imediato. Os conservacionistas podem ser radicais, defendendo proibições totais da extração, ou moderados, preferindo soluções de diálogo.
As comunidades locais também variam, com algumas dependentes da extração de madeira para sua subsistência, enquanto outras priorizam a preservação da floresta. Cada grupo possui crenças sobre as intenções dos outros; os madeireiros acreditam que os conservacionistas são, em sua maioria, moderados, enquanto os conservacionistas suspeitam que a maioria dos madeireiros age de forma irresponsável. As comunidades locais desenvolvem suas próprias crenças, que influenciam suas alianças.

As estratégias de cada grupo incluem, para os madeireiros, escolher entre extração intensiva, práticas sustentáveis ou negociação com comunidades; para os conservacionistas, decidir entre protestar, negociar ou envolver as comunidades em sua causa; e para as comunidades, optar por colaborar com madeireiros, apoiar conservacionistas ou buscar um equilíbrio entre os dois interesses.
Um possível equilíbrio de Bayes-Nash ocorre quando cada grupo adota a melhor estratégia com base nas crenças que tem sobre os outros. Se, por exemplo, os madeireiros optarem por atuar de forma sustentável, acreditando que os conservacionistas são rigorosos, e os conservacionistas decidirem negociar para evitar conflitos, isso pode resultar em soluções de gerenciamento sustentável para a Amazônia. Assim, a interação entre esses agentes mostra como suas decisões interligadas impactam o futuro do ecossistema.
Teoria dos Jogos e Sustentabilidade
Essa denominação abrange a análise das interações estratégicas entre diferentes agentes no contexto da sustentabilidade, considerando suas decisões e consequências. Subcategorias que podem ser exploradas:
1. Tipos de Jogos:
Jogos de Soma Zero vs. Somas Positivas
Na exploração de recursos naturais, um jogo de soma zero implicaria que o ganho de um agente corresponde à perda de outro. Porém, no caso da Amazônia, o ideal é pensar em **jogos de soma positiva**, onde os agentes podem cooperar para aumentar o valor total derivado dos recursos, como biodiversidade, água, madeira, e serviços ecossistêmicos, de modo que todos os participantes (incluindo a floresta e o clima global) saiam ganhando.
Historicamente, a exploração dos recursos naturais amazônicos era frequentemente vista sob a ótica de um jogo de soma zero, onde o ganho de um ator implicava necessariamente na perda de outro. No entanto, uma nova perspectiva tem emergido, que enxerga a Amazônia como um potencial jogo de soma positiva, onde a cooperação e a busca por soluções sustentáveis podem gerar benefícios mútuos para todos os envolvidos.
Considere uma situação em que uma comunidade ribeirinha depende da pesca, mas a crescente demanda por peixes ornamentais e a exploração madeireira ameaçam seus recursos. A empresa madeireira busca lucro, enquanto a comunidade busca preservar seus meios de subsistência. Essa situação, onde o ganho de um implica na perda do outro, é um exemplo clássico de jogo de soma zero.
Para que seja transformado esse jogo como de soma positiva mediação de um órgão ambiental e a participação ativa da comunidade e da empresa é extremamente importante. Neste caso, A comunidade, com o apoio técnico e financeiro, pode desenvolver projetos de aquicultura de espécies nativas, criando uma fonte de renda alternativa e reduzindo a pressão sobre os estoques naturais. : A área de floresta explorada pela empresa pode ser transformada em uma reserva particular do patrimônio natural, oferecendo serviços de ecoturismo e educação ambiental. A comunidade local pode ser envolvida na gestão da reserva, oferecendo serviços como guias turísticos e hospedagem. A empresa e a comunidade podem unir forças para implementar medidas de recuperação de áreas degradadas e de tratamento de efluentes, garantindo a qualidade da água e a preservação da biodiversidade. Nesse novo cenário, todos os envolvidos saem ganhando. Essa é a essência de um jogo de soma positiva, onde a cooperação e a busca por soluções inovadoras levam a resultados benéficos para todos.
Jogos Cooperativos e Não Cooperativos
Na Teoria dos Jogos, um jogo pode ser **cooperativo** (em que os participantes formam alianças e cooperam para maximizar os ganhos) ou **não cooperativo** (em que cada agente tenta maximizar seus próprios benefícios, sem colaborar). O cenário ideal para a Amazônia envolveria a cooperação entre governos, empresas e comunidades locais para garantir a exploração sustentável dos recursos.
Exemplo cooperativo: Acordos internacionais que protegem a floresta e incentivam práticas sustentáveis de uso dos recursos naturais. Isso poderia envolver países amazônicos cooperando com potências globais sob o guarda-chuva de acordos como o Acordo de Paris.
Exemplo não cooperativo: Um cenário onde empresas privadas competem para maximizar a extração de recursos a curto prazo, ignorando os impactos ambientais de longo prazo.
Acordos como o Acordo de Paris podem ser vistos como um exemplo de um “jogo cooperativo” em escala global. Países amazônicos podem cooperar com nações desenvolvidas para proteger a floresta e promover práticas sustentáveis. A colaboração entre esses países pode resultar em benefícios mútuos, como financiamento para projetos de conservação e desenvolvimento sustentável, demonstrando que a cooperação pode levar a um resultado de soma positiva
2. Dilemas e Paradoxos:
Dilema do Prisioneiro e Sustentabilidade
O **dilema do prisioneiro** é um clássico exemplo de como dois agentes, agindo racionalmente e sem cooperação, podem acabar em uma situação em que ambos perdem. Na Amazônia, se cada ator – seja um governo local, uma empresa madeireira ou uma comunidade indígena – decidir explorar os recursos naturais sem coordenação, o resultado pode ser o esgotamento desses recursos, como o desmatamento desenfreado e a degradação da biodiversidade.
Esse dilema pode ser resolvido através de – incentivos à cooperação -, como mecanismos de – pagamentos por serviços ambientais (PSA) e programas de – desenvolvimento sustentável – que alinhem os interesses de curto prazo (lucro) com a necessidade de preservação de longo prazo.

Um exemplo prático é a implementação de programas de PSA, onde proprietários de terras recebem compensações financeiras por manter áreas florestais intactas. Isso cria um cenário de “jogo cooperativo”, onde todos os participantes (governos, comunidades locais e empresas) podem se beneficiar da preservação da floresta, ao mesmo tempo em que evitam a degradação ambiental. O sucesso desses programas depende da colaboração entre os diferentes agentes envolvidos, alinhando interesses de curto e longo prazo
Equilíbrio de Nash e Sustentabilidade
O conceito de **equilíbrio de Nash** ocorre quando os jogadores escolhem a melhor estratégia considerando a estratégia dos outros jogadores, e nenhum deles tem incentivo para mudar sua estratégia individualmente. No contexto amazônico, atingir um equilíbrio de Nash que favoreça a sustentabilidade significaria que todos os atores teriam incentivos para adotar práticas de conservação porque o impacto negativo da exploração excessiva afetaria a todos.
– Exemplo: O equilíbrio pode ser alcançado se todos os países amazônicos implementarem políticas de conservação e fiscalização rigorosa, e empresas que exploram os recursos naturais adotarem práticas certificadas de manejo sustentável. Isso evita que um agente individual se beneficie da exploração descontrolada enquanto os outros tentam preservar a floresta.
3. Dinâmicas Evolutivas:
Jogos Evolutivos e Adaptativos
Na exploração da Amazônia, os agentes podem estar envolvidos em **jogos evolutivos**, onde suas estratégias mudam com o tempo em resposta ao comportamento dos outros. Isso é particularmente relevante quando se considera o impacto das **mudanças climáticas** e a pressão global por responsabilidade ambiental. As empresas que resistirem à mudança para práticas sustentáveis podem ser forçadas a se adaptar se governos impuserem regulamentos mais rígidos ou consumidores globais demandarem produtos ecologicamente corretos.
Incerteza e Jogos com Informação Incompleta
O ambiente amazônico é caracterizado por **incerteza** quanto aos impactos de longo prazo da exploração dos recursos. Jogos com **informação incompleta** ocorrem quando um ou mais agentes não têm todas as informações sobre os outros jogadores ou sobre o estado do ambiente. Nesse contexto, a tomada de decisão baseada em ciência e dados confiáveis sobre o impacto ambiental e social torna-se crucial.
Exemplo: Decisores podem não ter informações precisas sobre os efeitos do desmatamento em ciclos hidrológicos ou sobre o impacto da extração de recursos sobre as comunidades locais. A ausência dessa informação pode levar a decisões subótimas ou à exploração excessiva.
O desafio da academia Amazonense de Matemática
A teoria dos jogos é uma área da matemática aplicada que estuda comportamentos estratégicos entre jogadores em situações de interação. Ela combina conceitos de matemática, economia, ciência política, biologia e psicologia.
O estudo da teoria dos jogos no contexto do desenvolvimento sustentável é uma abordagem multidisciplinar que envolve interações complexas entre diversos stakeholders, como governos, empresas, comunidades e organizações não governamentais. Essa interação configura um cenário em que a análise de incentivos econômicos, políticas governamentais, normas sociais e percepções individuais é essencial para compreender decisões relativas ao uso de recursos naturais e à proteção ambiental.
Por meio de modelagens de cenários, são criadas simulações em que diferentes grupos interagem em contextos de uso de recursos e emissões de carbono, permitindo a identificação de estratégias que podem levar a resultados tanto sustentáveis quanto insustentáveis. A teoria dos jogos também possibilita a análise de stakeholders, na qual se busca entender os interesses e motivações envolvidos nas iniciativas de desenvolvimento sustentável, formulando estratégias que incentivem a cooperação e minimizem comportamentos egoístas. Além disso, essa abordagem é útil para explorar como alianças podem ser formadas entre diversas partes interessadas, favorecendo a colaboração em desafios globais, como as mudanças climáticas.
A aplicação da teoria dos jogos nos dilemas coletivos típicos do desenvolvimento sustentável, como a gestão de recursos hídricos, revela a dinâmica de incentivos que levanta a questão de como motivar um grupo a agir em benefício coletivo mesmo quando existe a tentação de optar por soluções individualistas. A formulação de políticas que utilizem modelos de teoria dos jogos pode ser uma estratégia eficaz para promover a sustentabilidade, criando incentivos que beneficiem todos os envolvidos em jogos de soma não zero.
Finalmente, a implementação de abordagens educacionais que utilizam a teoria dos jogos oferece uma oportunidade única de engajar públicos variados, utilizando jogos e simulações como ferramentas pedagógicas para ensinar sobre a importância da cooperação e das decisões sustentáveis. Uma tabela a seguir resume os conceitos matemáticos fundamentais aplicados a esses jogos;
Os cursos de matemática no Estado do Amazonas devem orientar suas práticas e conhecimentos para abordar os desafios específicos da região. Ao integrar outras áreas do conhecimento, esses programas têm o potencial de se tornarem referências globais em modelagem matemática voltada para o desenvolvimento sustentável da floresta tropical. Essa colaboração interdisciplinar favorecerá a elaboração de soluções inovadoras e eficazes, promovendo, assim, a preservação e o desenvolvimento sustentável da Amazônia.
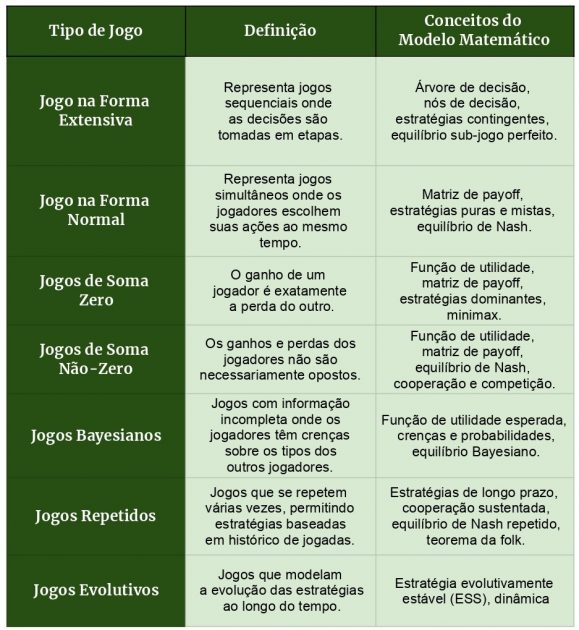
Conclusão
A teoria dos jogos também pode ser usada para modelar mecanismos de incentivo que promovam comportamentos sustentáveis. Por exemplo, subvenções governamentais para práticas agrícolas sustentáveis ou créditos de carbono para quem protege áreas florestais podem alinhar os interesses econômicos de curto prazo com a preservação ambiental.
A Amazônia enfrenta desafios significativos, como desmatamento e atividades agrícolas insustentáveis. Para lidar com esses problemas, a colaboração entre diversos agentes, como governos, comunidades locais, ONGs e empresas, é fundamental.
Um modelo que pode ser utilizado para entender essas interações é o “Dilema do Prisioneiro”. Nesse cenário, dois fazendeiros têm a opção de desmatar suas terras. Se ambos optarem pela preservação, eles garantem benefícios a longo prazo. No entanto, se um desmatar, ele obterá lucros imediatos, enquanto o outro perderá. Se ambos desmatarem, ambos podem ter lucro por um tempo, mas a floresta será destruída, resultando em um colapso futuro. Os Programas de pagamento por serviços ambientais (PSA) podem servir como incentivos para que os fazendeiros escolham a preservação em vez da destruição.
Outro modelo relevante é o “Jogo de Recursos Comuns”. Aqui, uma comunidade depende de um rio para sua subsistência. Se a maioria optar por usar o recurso de forma sustentável, todos se beneficiarão. Caso muitos decidam explorá-lo excessivamente, o recurso se esgotará, levando à escassez e a conflitos. A criação de comitês de gestão de recursos pode ajudar a promover a colaboração e a responsabilização entre os usuários. Além disso, os jogos evolutivos ilustram a interação entre espécies nativas e atividades humanas, destacando a importância de proteger a biodiversidade.
Em comunidades que dependem de um rio para sua subsistência, a Teoria dos Jogos pode ser aplicada para modelar a gestão sustentável da água. Se a maioria dos usuários optar por usar o recurso de forma sustentável, todos se beneficiam. No entanto, se muitos decidirem explorar excessivamente, o recurso se esgotará, levando a conflitos. A criação de comitês de gestão de recursos pode ajudar a promover a colaboração e a responsabilização entre os usuários, ilustrando a importância da cooperação
Incentivos fiscais e apoios financeiros para práticas agroecológicas podem encorajar a preservação das espécies nativas e o equilíbrio ecológico. Em suma, a teoria dos jogos oferece uma estrutura útil para entender a dinâmica entre agentes na Amazônia.
Por meio de incentivos adequados e da promoção da colaboração, é possível melhorar a gestão de recursos naturais e garantir a sustentabilidade a longo prazo da Amazônia.
Finalmente, os cursos das universidades do Estado do Amazonas poderiam abordar com a máxima consistência a Teoria dos Jogos aplicada à exploração racional dos recursos naturais da Amazônia. Ao modelar os interesses de diversos atores – desde empresas até comunidades locais – é possível criar cenários onde o desenvolvimento econômico e a preservação ambiental caminhem juntos. Estratégias baseadas em cooperação, criação de incentivos corretos e compartilhamento de informações podem ser ferramentas valiosas para proteger a Amazônia e garantir seu uso sustentável para gerações futuras.
Referências:
- Waldegrave, J. (1713). Carta sobre a solução de estratégia mista para o jogo le Her.
- Cournot, A. A. (1838). Researches into the Mathematical Principles of the Theory of Wealth.
- Von Neumann, J., & Morgenstern, O. (1944). The Theory of Games and Economic Behavior.
- Nash, J. (1950). Equilíbrio de Nash.
- Selten, R. (1965). Equilíbrio perfeito em sub-jogo.
- Harsanyi, J. (1967). Jogos Bayesianos.
- Smith, J. M. (1970). Estratégia evolutivamente estável.
- Schelling, T., & Aumann, R. (2005). Contribuições à teoria dos jogos
[1] HUZINGA, Johan. Homem ludens. Tradução de João Paulo Monteiro. Revisão de Mary Amazonas Leite de Barros. São Paulo: Perspectiva, 1971.
[2] Von Neumann, J., & Morgenstern, O. (1944). Theory of Games and Economic Behavior. Princeton University Press
[3] Nash, J. (1950). Equilibrium points in n-person games. Proceedings of the National Academy of Sciences, 36(1), 48-49.

















